Botlab

Table of Contents

• Table of Contents
• PART1: Motion \& Odometry
  • 1.1 Characterize Wheel Speed for a Open Loop Controller
  • 1.2 Wheel Speed Open Loop \& PID Controller
  • 1.3 Odometry
  • 1.4 Gyro Sensor Fusion
  • 1.5 Robot Frame Velocity Controller
  • 1.6 Drive Square (this step is in preparation for 1.7)
  • 1.7 Motion Controller
  • Part 1 Checkpoint Maze Example
• PART 2: SLAM
  • LCM Logs
  • Accounting for Scan Speed
  • 2.1 Mapping - Occupancy Grid
  • 2.2 Monte Carlo Localization
    • 2.2.1 MCL - Action Model
    • 2.2.2 MCL - Sensor Model \& Particle Filter
  • 2.3 Simultaneous Localization and Mapping (SLAM)
  • Part 2 Checkpoint
• PART 3: Implementing Planning and Exploration
  • 3.1 Obstacle Distance
  • 3.2 A* Path Planning
  • 3.3 Map Exploration
  • 3.4 Map Localization with Unknown Starting Position

PART1: Motion & Odometry

We want to be able to control the robot’s position, but to do this we need to be able to tell the robot how to move. The control signal we have to move the robot is a motor PWM command, which effectively commands how much effort we wish the motors to produce. However, it would be most convenient to be able to command the velocities of the robot from a higher level in order to move the robot in the environment. One simple way to control the robot speed is to control the speed of each wheel. This can be accomplished in a few different methods. One method is to set the motor PWM based on a function that you determine will produce the desired wheel speed. This is called an open loop because there is no feedback. This is the least accurate way of controlling the speed. A better method would be to use encoder data to control the wheel speed using a feedback controller. The goal of this part of the lab will be to build an increasingly sophisticated robot controller, and at the end take quantitative data to compare them. Additional hints/instructions can be viewed HERE.

1.1 Characterize Wheel Speed for a Open Loop Controller

Follow the instructions below to characize your motors. This will involve building the firmware, flashing the pico, and taking the output and saving this into a .csv file (or google doc). You can use this data to run linear regression.

Required For the Report:

• Report the motor calibrations (intercept and slope parameters) for the robot on a concrete floor (or a floor mat, if you are using one) for as many of the teams’ robots as you can (minimum two different robots). Note that once you calibrate it on a certain surface, please use the same surface for all the following tasks (so that your calibration parameters will be accurate).
• Plot of the motor speed vs. pwm for the loaded wheels and fitted curve. You should calibrate for both wheels. Please remember to label both axes and title of your plot. Here, the x-data will be the speed, and the y-data will be the PWM.

Please include discussions on:

• How much variation is there in the calibration functions between left and right wheel? Between different bots within your group?
• What do you think is the source of variation?

1.2 Wheel Speed Open Loop & PID Controller

Within mbot-controller-pico/src/mbot.c, create two controllers, one to control each wheel velocity using your open loop calibration, and one to control each wheel’s speed using PID controllers. The controllers should keep the wheels moving the desired speed so the robot moves in as straight a line as possible without heading correction, but likely this won’t be perfect. Observe these controllers and compare their behavior and then either choose one of them or use these controllers as a starting point for a more sophisticated controller.

Other features you could consider adding/changing for your controller:

• Combine the feed forward (FF) and feedback (FB) controllers by adding the outputs. This way the PID needs only to correct for the error between the measured speed and calibration function, reducing or eliminating the need for an integral term.
• Use a low-pass filter on the wheel velocity estimates, this will reduce the discretization noise caused by the encoder resolution.
• Slow down the rate that you are running the controller by changing the SAMPLE_RATE_HZ and corresponding DT #define parameters. (25/.04 & 20/.05 might be more suitable)
• Use a low-pass filter on the setpoints, this will slow the acceleration & deceleration of the robot (no more face plants)

You can modify the previous python scripts from the Intro & Setup assignment to generate velocity commands to test your controller. Remember, this will require running the shim and timesync binaries.

Required For the Report:

• Implement the following controllers on your MBot:
  • CASE 1 (required): open loop controller (feed forward only)
  • CASE 2 (required): Simple Basic Wheel Speed PID
  • (optional) try add low-pass filters or any other features above to modify your controller
• Describe your controllers in the report. Provide any associated step response plots.
• Give a table of parameters (gains, filter parameters etc.) for the controller.

Please include discussions on:

• How do the two simple controllers compare?
• How did you tune the parameters in your controller? What metric did you use to decide it was sufficiently tuned?
• What additional features beyond the simplest PID filter did you implement and what were the effects?

1.3 Odometry

Implement the odometry functions in mbot-controller-pico/src/mbot.c to calculate the robots position and orientation and enable dead reckoning with wheel encoders only. You should test your implementation by manually moving the robot by known distances and turning by known angles. If you are unsatisfied with the accuracy of the odometry, try a calibration procedure such as UMBark.

Required For the Report:

• Implement the odometry functions in the code. Describe how you validated your odometry model and report the values of correction parameters (if any).

1.4 Gyro Sensor Fusion

Add another macro GYRODOMETRY to mbot-controller-pico/src/mbot.h that can either be set to 0 or 1. Modify your odometry code to check for the value of this variable. When it is false, run the standard odometry. When it is true, implement the gyro sensor fusion.

Either implement the “gyrodometry” algorithm discussed in lecture or implement your own algorithm for fusing the gyro data with odometry data for estimating the heading of the Mbot.

Hint: The preferred way to read \(\Delta\theta_{gyro}\) is by taking the difference between consecutive samples of tb_angles.

Required For the Report:

• Write out the equations used to perform odometry and gyro fused odometry. (In mathematical notation and/or pseudo code, no need to put in actual code in report)
• Report all parameters in your odometry and gyrodometry model.
• Describe how the parameters were determined.

Note: If you feel like you can completely ignore the IMU for heading information or alternatively completely ignore the odometry, you should describe this in your report, and include your experimental data to justify your decision.

1.5 Robot Frame Velocity Controller

Modify the robot frame velocity on top of the PID controller in mbot-controller-pico/src/mbot.c For this, instead of the set point velocity being determined by the motor command, this will be determined by a another PID comparing the current measured velocity and the target.

This can then be tested by modifying the script botlab/python/step_test.py to create different trajectories within Python. You can also test this further by developing the motion controller in Section 1.6.

Required For the Report:

• Implement the following controllers on your MBot:
  • CASE 3 (required): wheel speed PID with both forward and turning velocity setpoints AND at least one of the following
  • CASE 4: open loop controller + wheel speed PID
  • CASE 5: advanced wheel speed PID with saturated integral term
  • CASE 6: advanced wheel speed PID with low pass filters
  • CASE 7: “All the Things” as in the lecture notes, add all the above
  • CASE 8: Any other modifications you find useful

Note that, the ultimate goal is for you to have a working controller that will control your bot in a precise way, so you may need to experiment with several controllers and see how they behave and choose one that behaves the best for your robot.

• Describe which robot frame velocity controller you have implemented in the report. Include a block diagram.
• Give a table of parameters (gains, filter parameters etc.) for the controllers.
• Generate a plot of robot x position (robot frame) vs time for the following step inputs:
  • 0.25 m/s for 2s
  • 0.5 m/s for 2s
  • 1 m/s for 1s
• Generate a plot of robot frame heading vs time for the following step inputs:
  • \(\pi/8\) rad/s for 2s
  • \(\pi/2\) rad/s for 2s
  • \(\pi\) rad/s for 2s

1.6 Drive Square (this step is in preparation for 1.7)

Modify the python script botlab/python/step_test.py to create a new timed drive for executing a square. Build off of this script, as it has a slightly different format for sending motion commands than the Python motor commands in the Teleop Pico introduction assignment.

Required For the Report:

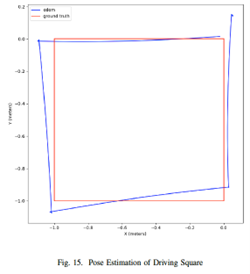
• Include a plot of your robot’s dead reckoning estimated pose as the robot is commanded to drive a 1m square 1 time. Your plot may look something like this (though hopefully more accurate!)
• Include a plot of the robots linear and rotational velocity as it drives one loop around the square.
• Discuss how this timed drive square compares to the timed drive square you implemented in the Setup/Introduction assignment.

1.7 Motion Controller

Finally, design your motion controller for driving between waypoints of type pose_xyt_t and implement it in botlab/src/mbot/motion_controller.cpp in the botlab repository. This program will run on the RPi. Your motion controller should take in messages of type robot_path_t on the channel CONTROLLER_PATH and execute the trajectory until the robot reaches the final waypoint.

We have provided a template for sending pose commands through the program botlab/src/mbot/drive_square.cpp. You can use this script to tune the PID of the motion controller, as well as copy it as a template for giving waypoints of an arbitrary path.

You may need to tune the PID controller within botlab/src/mbot/motion_controller.cpp You can also tune the limits for the forward velocity and angular velocity to balance the speed and accuracy of your motion controller. Modify these values at the bottom of botlab/src/mbot/motion_controller.cpp

Required For the Report:#

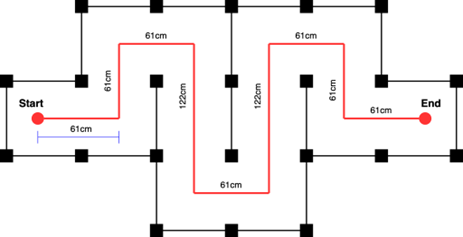
• Demonstrate your motion controller by having it drive the illustrated path in one of the mazes set up in the lab (see an example of the checkpoint maze below; OR, you can set up your own maze of some complexity– not just drive square). Record a video of the robot attempting the path at a slow speed (e.g., ~0.2m/s & pi/4 rad/s) and at a high speed (e.g., ~0.8m/s, pi rad/s) and provide a link to these two videos (make sure the instructors have access). The velocity limits hardcoded on motion_controller.cpp are hardcoded to be slower than the high speed for students getting started. To test the high speed, you can modify these limits.
• Produce a plot of the (x,y) odometry position as the robot executes the path at both speeds.
• Discuss the motion control system you implemented on the MBot. Which controller ended up performing the best? How did you tune the PID parameters and the velocity limits?

Part 1 Checkpoint Maze Example

PART 2: SLAM

During the SLAM part of the lab , you will build an increasingly sophisticated algorithm for mapping and localizing in the environment. You will begin by constructing an occupancy grid using known poses. Following that, you’ll implement Monte Carlo Localization in a known map. Finally, you will put each of these pieces together to create a full SLAM system. Much of this can be initiated using only logs and when you are ready to use the actual robot.

To run the botgui:

pi@raspberrypi:~ $ cd botlab
pi@raspberrypi:botlab $ source setenv.sh
pi@raspberrypi:botlab $ ./bin/botgui

LCM Logs

For this phase, we have provided two LCM logs containing sensor data from the MBot along with ground-truth poses as estimated by the staff’s SLAM implementation.

• data/convex_10mx10m_5cm.log: convex environment, where all walls are always visible and the robot remains stationary (use for initial testing of algorithms).
• data/drive_square_10mx10m_5cm.log: a convex environment while driving a square
• data/obstacle_slam_10mx10m_5cm.log: driving a circuit in an environment with several obstacles

To play back these recorded LCM sessions on a laptop (with Java), you can use the lcm-logplayer-gui

$ lcm-logplayer-gui data/convex_10mx10m_5cm.log

Note: you can also run the command line version, lcm-log-player, if the system does not have Java. In the GUI version you can turn off LCM channels with a checkbox. The same functionality is available in the command line version, check the help with

$ lcm-logplayer --help

You will need to turn off the LCM channel SLAM_MAP to visualize the results of your mapping implementation.

Similarly, to record your own lcm logs, for testing or otherwise, you can use the lcm-logger

$ lcm-logger -c SLAM_POSE_CHANNEL my_lcm_log.log 

This example would store data from the OPTITRACK_CHANNEL in the file my_lcm_log.log. With no channels specified, all channels will be recorded over the interval.

Accounting for Scan Speed

The laser rangefinder beam rotates in 360 degrees at a sufficiently slow rate such that the robot may move a non-negligible distance in that time. Therefore, you will need to estimate the actual pose of the robot when each beam was sent in order to determine the cell in which the beam terminated. To do so, you must interpolate between the robot pose estimate of the current scan and the scan immediately before. Remember that the pose estimate of the previous SLAM update occurred immediately before the current scan started. Likewise, the pose estimate of the current SLAM update will occur when the final beam of the current scan is measured. We have provided code to handle this interpolation for you, which is located in src/slam/moving_laser_scan.hpp. You only need to implement the poses to use for the interpolation.

2.1 Mapping - Occupancy Grid

Implement the occupancy grid mapping algorithm in the Mapping class in slam/mapping.cpp/.hpp.

An occupancy grid describes the space around the robot via the probability that each cell of the grid is occupied or free. We will use a grid with at most 10 cm cells, whose log-odds values are integers in the range [-127,127]. To perform the ray casting on your occupancy grid you might want to implement Breshenham’s line algorithm as described in class lecture.

For this Task, use the ground-truth poses in the provided log files to construct occupancy grid maps of each one. Using the poses from the log file is handled by specifying the –mapping-only command-line option when you run the slam program.

Required For the Report:

• Plot of your map from the log file obstacle_slam_10mx10m_5cm.log.

2.2 Monte Carlo Localization

As discussed in lecture, Monte Carlo Localization (MCL) is a particle-filter-based localization algorithm. Implementation of MCL requires three key components: an action model to predict the robot’s pose, a sensor model to calculate the likelihood of a pose given a sensor measurement, and various functions for particle filtering including drawing samples, normalizing particle weights, and finding the weighted mean pose of the particles. You will implement MCL using odometry, laser scans, and an occupancy grid map.

In these tasks, you’ll run the slam program in localization-only mode using a saved map. Use the ground-truth maps provided with the sensor logs. You can run slam using: ./slam --localization-only <filename>.

To test the action model only, you can run in action-only mode with localization-only turned on: ./slam --localization-only <filename> --action-only.

2.2.1 MCL - Action Model

Implement an action (or motion) model using odometry or wheel encoder data. The skeleton of the action model can be found in slam/action_model.h/.cpp.

Refer to Chapter 5 of Probabilistic Robotics for a discussion of common action models. You can base your implementation on the pseudo-code in this chapter. There are two action models that are discussed in detail, The Velocity Model (Sec. 5.3) and the Odometry Model (Sec. 5.4).

Required For the Report:

• Describe the action model you used. Include the equations you used
• Include a table of the values of any uncertainty parameters.
• Explain how you chose these values.

2.2.2 MCL - Sensor Model & Particle Filter

Implement a sensor model that calculates the likelihood of a pose given a laser scan and an occupancy grid map. The skeleton of the sensor model can be found in slam/sensor_model.h/.cpp.

Refer to Chapter 6 of Probabilistic Robotics for a discussion of common sensor models. You can base your implementation on the pseudo-code in this chapter.

Finish implementing the particle filter contained in slam/particle_filter.h/.cpp.

Refer to Chapter 4 of Probabilistic Robotics for help in implementing your particle filter.

Hint: In case of a slow performance of your sensor model, consider increasing the ray stride in the MovingLaserScan call.

Required For the Report:

• Report in a table the time it takes to update the particle filter for 100, 300, 500 and 1000 particles. Estimate the maximum number of particles your filter can support running at 10Hz on the RPi.
• Using your particle filter on the log drive_square_10mx10m_5cm.log, plot 300 particles at the midpoint of each 1m translation and at the corners after having turned 90°
• Provide a separate plot showing how the pose error difference between the SLAM and Odometry poses evolves over time.

2.3 Simultaneous Localization and Mapping (SLAM)

You have now implemented mapping using known poses and localization using a known map. You can now run the slam program in SLAM mode, which uses the following simple SLAM algorithm:

• Use the first laser scan received to construct an initial map.
• For subsequent laser scans:
  • Localize using the map from the previous iteration.
  • Update the map using the pose estimate from your localization.

NOTE: The above logic is already implemented for you. Your goal for this task is to make sure your localization and mapping are accurate enough to provide a stable estimate of the robot pose and map. You will need good SLAM performance to succeed at the robot navigation task.

Required For the Report:

• Create a block diagram of how the SLAM system components interact
• Compare the estimated poses from your SLAM system against the ground-truth poses in obstacle_slam_10mx10m_5cm.log. Use this to estimate the accuracy of your system and include statistics such as RMS error etc.

Part 2 Checkpoint

• Demonstrate your SLAM system by mapping the maze used for Checkpoint 1. Above, we show one example of the maze, but you are also welcome to create your own maze (should have some complexity beyond a simple drive square).
• You may either manually drive the path with teleop, click to drive in botgui, or try using your python script from checkpoint 1.
• Submit a screenshot of the map, showing the SLAM_PATH and ODOMETRY_PATH taken (turn off lasers, & frontiers)
• Submit a lcm log file of the run and a .map file as well (you can uncomment the line map_.saveToFile(“current.map”); in slam.cpp to output maps)
• Write a short description of your SLAM system and any features we should be aware of.

PART 3: Implementing Planning and Exploration

Using the SLAM algorithm implemented in part 1, you can now construct a map of an environment using the MBot simulator. Now you will implement additional capabilities for the MBot: path planning using A* and autonomous exploration of an environment.

3.1 Obstacle Distance

The robot configuration space is implemented in planning/obstacle_distance_grid.h/.cpp. Run obstacle_distance_grid_test and check if your code passes the three tests. The botgui already has a call for a mapper object from which it can obtain and draw an obstacle distance grid. You can view the generated obstacle distance grid by ticking “Show Obstacle Distances” in botgui.

3.2 A* Path Planning

Write an A* path planner that will allow you to find plans from one pose in the environment to another. You will integrate this path planner with the motion_controller from Phase 2 to allow your MBot to navigate autonomously through the environment.

For this phase, you will implement an A* planner and a simple configuration space for the MBot. The skeleton for the A* planner is located in planning/astar.h/.cpp Your implementation will be called by the code in planning/motion_planner.h/.cpp. You can test your astar_test code using botgui, check astar_test code for appropriate arguments.

Once your planner is implemented, test it by constructing a map using your SLAM algorithm and then using botgui to generate a plan. Right-click somewhere in free space on your map. Your planner will then be run inside botgui and a robot_path_t will be sent to the motion_controller for execution.

astar_test & astar_test_files can be used to test the performance of your A* planner.

Required For the Report:

• Provide a figure showing the planned path in an environment of your creation with the actual path driven by your robot overlayed on top.
• Using astar_test_files, report statistics on your path planning execution times for each of the example problems in the data/astar folder – you simply need to run astar_test_files after implementing your algorithm. If your algorithm is optimal and fast, great. If not please discuss possible reasons and strategies for improvement.

3.3 Map Exploration

Up to now, your MBot has always been driven by hand or driven to goals selected by you. For this task, you’ll write an exploration algorithm that will have the MBot autonomously select its motion targets and plan and follow a series of paths to fully explore an environment.

We have provided an algorithm for finding the frontiers – the borders between free space and unexplored space – in planning/frontiers.h/.cpp. Plan and execute a path to drive to the frontier. Continue driving until the map is fully explored, i.e. no frontiers exist. Once you have finished exploring the map, return to the starting position. Your robot needs to be within 0.05m of the starting position. The state machine controlling the exploration process is located in planning/exploration.h/.cpp.

Required For the Report:

• Explain the strategy used for finding frontiers and any other details about your implementation that you found important for making your algorithm work.

3.4 Map Localization with Unknown Starting Position

For the competition task, you will be asked to localize on a map where you do not know your initial position. This will require initializing your particles uniformly in open space on the map. Then you will need a way to move from this unknown location without hitting obstacles and without the use of your A* planner in order to update your localization estimate until your distribution is narrow enough to know where you are.

Required for report:

• Explain the strategy used for localization in this instance and any other details about your implementation that you found important for making your algorithm work.